Question

rodney+invests+$2,400+today,+compounded+monthly,+with+an+apr+of+4.23%.+what+is+rodney's+investment+worth+in+one+year?+group+of+answer+choices+$2,503.57+$2,532.00+$2,554.37+$2,515.66

Answer 1

Rodney's investment is worth approximately $2,503.57 in one year.

Step-by-step explanation:

To calculate Rodney's investment worth in one year, we can use the formula for compound interest:

`A = P(1 + r/n)^n^t`

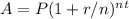
Where:
A = the future value of the investment
P = the principal amount (initial investment)
r = the annual interest rate (in decimal form)
n = the number of times the interest is compounded per year
t = the number of years

In this case, Rodney invests $2,400 today at an APR of 4.23%, compounded monthly. Therefore:
P = $2,400
r = 4.23% = 0.0423
n = 12 (compounded monthly)
t = 1 year

Substituting these values into the formula, we get:

`A = 2400(1 + 0.0423/12)^(^1^2^ *^ 1^)`

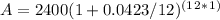
Calculating this expression gives us the final value of Rodney's investment after one year, which is approximately $2,503.57.