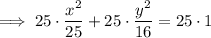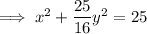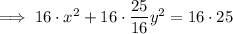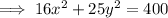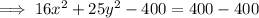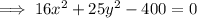Answer:
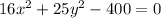
Explanation:
Given:
- The sum of the distance of any point (x, y) in this conic to the two focuses F₁=(-3,0) and F₂=(3, 0) is constant and equal to 10.
There are 4 types of conic sections:
- Circles (one focus).
- Parabolas (one focus).
- Ellipses (two foci).
- Hyperbolas (two foci).
The definition of an ellipse is:
- The set of points in a plane such that the sum of the distance from a point to each focus is constant.
Therefore, the given definition is one for an ellipse.

As the given foci are (-3, 0) and (3, 0), they are on the x-axis. Therefore:
Therefore, the major axis is on the x-axis and the vertices are (h±a, k) and the co-vertices are (h, k±b).
The constant is the major axis which is 2a. Given the constant is 10:

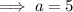
Since c² = a² - b²:
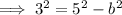
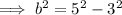
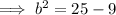
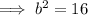
Therefore, the equation for the conic section (ellipse) is:
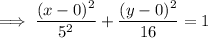
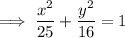
In standard form: