Answer:
By closure property of multiplication and addition of integers,
If
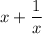 is an integer
is an integer
∴
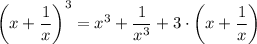 is an integer
is an integer
From which we have;
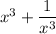 is an integer
is an integer
Explanation:
The given expression for the positive integer is x + x⁻¹
The given expression can be written as follows;
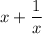
By finding the given expression raised to the power 3, sing Wolfram Alpha online, we we have;
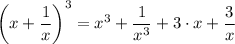
By simplification of the cube of the given integer expressions, we have;
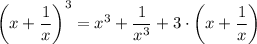
Therefore, we have;
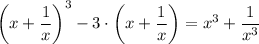
By rearranging, we get;
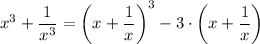
Given that
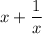 is an integer, from the closure property, the product of two integers is always an integer, we have;
is an integer, from the closure property, the product of two integers is always an integer, we have;
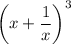 is an integer and
is an integer and
 is also an integer
is also an integer
Similarly the sum of two integers is always an integer, we have;
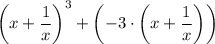 is an integer
is an integer
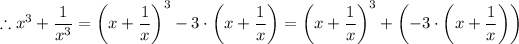 is an integer
is an integer
From which we have;
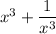 is an integer.
is an integer.