Answer:
The value of j = -5
Explanation:
Given the points of the line
Slope m = -1
To determine the value of j, we need to use the slope formula
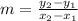
Here:
Now, substitute (x₁, y₁) = (j, -9) and (x₂, y₂) = (-10, -4) in the formula

We are already given m = -1. Therefore, we need to substitute m = -1 in the formula and solve for j
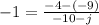
Multiply both sides by -10 - j
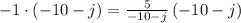
Simplify
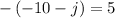
Divide both sides by -1
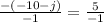
Simplify
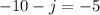
Add 10 to both sides

Simplify
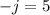
Divide both sides by -1
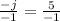
Simplify
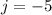
Therefore, the value of j = -5
Verification:
As the value of j = -5
Now we have the points
Now, we need to check whether the slope between the points (-5, -9) and (-10, -4) is -1 or not.
Let us determine the slope between the points (-5, -9) and (-10, -4)
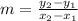
Here:
Now, substitute (x₁, y₁) = (-5, -9) and (x₂, y₂) = (-10, -4) in the formula
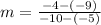
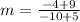
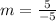
Apply fraction rule:
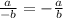
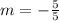
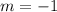
Therefore, we verified that the slope of the line containing the points (-5, -9) and (-10, -4) is indeed m = -1.