Question

. determine r and all possible values of the argument, θ, for the following. also, sketch z on the complex plane, clearly labeling the angles and two axes.

Answer 1

In polar coordinates, a complex number can be represented as a distance from the origin (r) and an angle (θ) it makes with the positive x-axis. To determine the values of r and θ, use the relationships between the real and imaginary parts of the complex number. To sketch the complex number on the complex plane, plot the point (a, b) and draw a line from the origin to the point, labeling the angle θ.

Step-by-step explanation:

In polar coordinates, a complex number can be represented as a distance from the origin (r) and an angle (θ) it makes with the positive x-axis. To determine the values of r and θ, you can use the relationships between the real and imaginary parts of the complex number.

For example, if you have a complex number in the form z = a + bi, where a is the real part and b is the imaginary part, you can calculate r using the formula
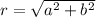`r = √(a^2 + b^2)` and θ using the formula
`\theta = tan^(^-^1^)(b/a)`.

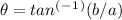To sketch the complex number z on the complex plane, you can plot the point (a, b) where a represents the real part and b represents the imaginary part. Then, draw a line from the origin to the point (a, b) to represent the distance r. Finally, label the angle θ at the end of the line to complete the sketch.