Question

Choose one of the two boxes at random. Then select one of the balls in this box at random. If a red ball is selected, what is the probability that this ball is from the first box?

Answer 1

The probability that the red ball selected is from the first box is
`\((1)/(3)\).`

Step-by-step explanation:

Let
`\(A\)`be the event that the red ball is selected and
`\(B\)`be the event that the ball is from the first box. We need to find
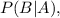`\(P(B|A)\),` the conditional probability of
`\(B\)` given
`\(A\).`

By Bayes' Theorem,
`\(P(B|A) = (P(A|B) \cdot P(B))/(P(A))\).`

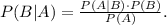
Here,
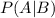`\(P(A|B)\)` is the probability of selecting a red ball given that it's from the first box, which is
`\(1\). \(P(B)\)` is the probability of choosing the first box, which is
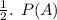`\((1)/(2)\). \(P(A)\)` is the probability of selecting a red ball, and it can happen in two ways: either from the first box
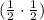`(\((1)/(2) \cdot (1)/(2)\))`or from the second box
`(\((1)/(2) \cdot (1)/(2)\)), so \(P(A) = (1)/(4) + (1)/(4) = (1)/(2)\).`

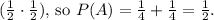
Substituting these values into Bayes' Theorem:

`\[P(B|A) = (1 \cdot (1)/(2))/((1)/(2)) = (1)/(3).\]`

Therefore, the probability that the red ball selected is from the first box is
`\((1)/(3)\).` This result may seem counterintuitive at first, but it highlights the importance of conditional probabilities in situations with multiple stages of randomness.: