Final Answer:
The value of x in the intervals for the equation
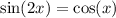 is
is
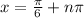 , where
, where
 is an integer.
is an integer.
Step-by-step explanation:
To find the value of
 in the given equation,
in the given equation,
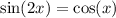 , we can use trigonometric identities. First, let's rewrite the equation using double-angle and basic trigonometric identities:
, we can use trigonometric identities. First, let's rewrite the equation using double-angle and basic trigonometric identities:
![\[ \sin(2x) = \cos(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lngc8m2cdk2pa6uc4ac6bycvxldhylg0qq.png)
Using the double-angle identity
 , we get:
, we get:
![\[ 2\sin(x)\cos(x) = \cos(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f3cm8uctksiqaecjwn17m6pggqwwi1j205.png)
Now, we can simplify by dividing both sides by
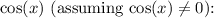
![\[ 2\sin(x) = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/daxqsxtfepucgkkwsgie3i7jlptwgg67fu.png)
Dividing both sides by 2:
![\[ \sin(x) = (1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/73lrkp4vgk0nbxp54env44m6dlblveg4sx.png)
This gives us
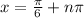 , where
, where
 is an integer. The solution is periodic because the sine function repeats every
is an integer. The solution is periodic because the sine function repeats every
 radians.
radians.
In conclusion, the solution to the equation
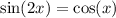 is
is
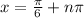 , where
, where
 can take any integer value. This represents the intervals in which the equation holds true, considering the periodic nature of trigonometric functions.
can take any integer value. This represents the intervals in which the equation holds true, considering the periodic nature of trigonometric functions.