The beam is supported by a pin at point A and a horizontal roller at point D. There are two unknown reactions at point A and one at point D as shown below.
What inform the reactions at the supports?
As shown in the free-body diagram, there are three unknown reactions that need to be solved for using the equilibrium condition. Since this represents a two-dimensional force system, we can only make use of three equilibrium equations.
We begin the solution by using the equilibrium of moments with point A as the moment center. This is because point A contains two out of three unknown reactions.
Σ
= 0
-60(1.5) - 50 (4.5) +
(5.5) = 0
= 57.3 KN ↑
Positive sign on the reaction indicates its assumed direction is correct. Now we proceed with solving the remaining two reaction forces. Using the equilibrium of forces in the x direction gives
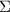
= 0
=>
= 0
The horizontal reaction force at A is zero as there is no other horizontal force acting on the beam.
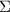
= 0
- 60 - 50 +
= 0
=>
= 52.7 KN ↑