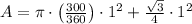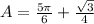Question

Find the area of the shaded region in the figure below.

I've found the total circle area as per the sector formula, which is pi but from there I'm kinda lost.
Please see the image below. If possible, please attach your work as well (I don't want to copy anyone and would prefer to learn it)

Answer 1

The area of the shaded region is equal to
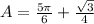`A = (5\pi)/(6) + (√(3))/(4)`. (Correct choice: 2).

How to determine the area of a shaded region

In this problem we must find the exact value of a shaded region seen in the figure, consisting in summing the areas of a circular sector and a equilateral triangle, whose area formulas are, respectively:

Circular sector:

`A = \pi \cdot \left((\theta)/(360) \right)\cdot r^2`

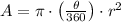
Where:

• r - Radius, in units.
• θ - Central angle, in degrees.

Equilateral triangle:

`A = (√(3))/(4) \cdot a^2`

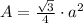
Where a is the side length of the equilateral triangle.

If we know that θ = 300º, a = r = 1, then the area of the shaded area is equal to:

`A = \pi \cdot \left((300)/(360) \right)\cdot 1^2 + (√(3))/(4)\cdot 1^2`

`A = (5\pi)/(6) + (√(3))/(4)`