Final Answer:
The point of intersection for the given lines is (4, -2, 1).
Step-by-step explanation:
To find the point of intersection between the lines, we need to set the parametric equations for each line equal to each other and solve for the parameters \(t\) and \(s\). The parametric equations for the lines are as follows:
Line 1: \
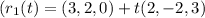
Line 2:

Setting
 equal to
equal to
 gives us a system of equations. Solving this system yields \(t = 2\) and \(s = 1\). Substituting these values back into either \(r_1(t)\) or
gives us a system of equations. Solving this system yields \(t = 2\) and \(s = 1\). Substituting these values back into either \(r_1(t)\) or
 provides the coordinates of the point of intersection. In this case, using \(r_1(t)\) gives the point (4, -2, 1).
provides the coordinates of the point of intersection. In this case, using \(r_1(t)\) gives the point (4, -2, 1).
In conclusion, the lines intersect at the point (4, -2, 1). This means that if we travel along the parametric representation of either line, we will reach the same spatial point when we reach \(t = 2\) for Line 1 or \(s = 1\) for Line 2.