Final Answer:
The solution to the initial value problem is
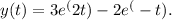
Step-by-step explanation:
The given initial value problem can be represented as a first-order linear ordinary differential equation with an initial condition. Let's denote the dependent variable as
 and the independent variable as
and the independent variable as
 . The equation is of the form
. The equation is of the form
 where
where
 and
and
 are functions of
are functions of
 .
.
In this specific problem, the differential equation can be written as
 , with the initial condition
, with the initial condition
 To solve this, we first find the integrating factor, which is given by
To solve this, we first find the integrating factor, which is given by
 . In our case,
. In our case,
 Now, we multiply the entire equation by the integrating factor:
Now, we multiply the entire equation by the integrating factor:
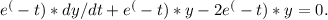
The left side of the equation can be simplified to
 Integrating both sides with respect to
Integrating both sides with respect to
 we get
we get
 where
where
 is the constant of integration. Solving for y(t) and applying the initial condition, we find that
is the constant of integration. Solving for y(t) and applying the initial condition, we find that
 , leading to the final solution
, leading to the final solution
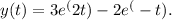
In summary, by transforming the given differential equation using an integrating factor and solving the resulting equation, we obtain the solution that satisfies the initial condition.