Question

Let h(x) = f(x)g(x). If f(x) = 5cos(x) and g(x) = 4x³ - 3x² + x + 1, what is h'(x)?

Answer 1

To find the derivative of
`\( h(x) = f(x)g(x) \)`, where
`\( f(x) = 5\cos(x) \)` and
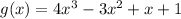`\( g(x) = 4x^3 - 3x^2 + x + 1 \)`, we use the product rule. The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. Applying this rule to ( h(x) ), we get
`\[ h'(x) = -20x^2\sin(x) + 30x\cos(x) + 5\cos(x)(12x^2 - 6x + 1) \]`.

Explanation:

The derivative
`\(h'(x)\)` of the function
`\(h(x) = f(x)g(x)\)`, where
`\(f(x) = 5\cos(x)\)` and
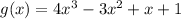`\(g(x) = 4x^3 - 3x^2 + x + 1\)`, is calculated using the product rule. The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. Applying this rule to the given functions, we get the following expression for (h'(x)):

`\[ h'(x) = -20x^2\sin(x) + 30x\cos(x) + 5\cos(x)(12x^2 - 6x + 1) \]`

In the first term,
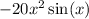`\(-20x^2\sin(x)\)`, we find the derivative of
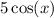`\(5\cos(x)\)` (the first function) multiplied by (g(x)) (the second function). In the second term,
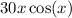`\(30x\cos(x)\)`, we have the product of (f(x)) and the derivative of (g(x)). The third term involves the product of (f(x)) and (g(x))'s derivative, which is
`\(12x^2 - 6x + 1\)`.

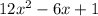Understanding the product rule is crucial in calculus as it provides a systematic method for finding the derivative of a product of functions. It is particularly useful in scenarios where functions are interdependent, and their rates of change need to be analyzed simultaneously.