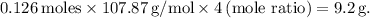Final answer:
The mass of silver (Ag) produced when 14.6 g of silver oxide (Ag₂O) undergoes the given reaction is 9.2 g.
Step-by-step explanation:
In the balanced chemical equation
 , it's evident that two moles of silver oxide (Ag₂O) yield four moles of silver (Ag). To find the molar mass of Ag₂O, we sum the atomic masses of silver (Ag) and oxygen (O). The molar mass of Ag₂O is
, it's evident that two moles of silver oxide (Ag₂O) yield four moles of silver (Ag). To find the molar mass of Ag₂O, we sum the atomic masses of silver (Ag) and oxygen (O). The molar mass of Ag₂O is
 which equals
which equals
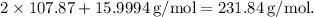
Now, we can calculate the moles of Ag₂O in 14.6 g using the formula:
 . Substituting the values, we get
. Substituting the values, we get
 . Since the mole ratio between Ag₂O and Ag is 1:2, the moles of silver formed is
. Since the mole ratio between Ag₂O and Ag is 1:2, the moles of silver formed is
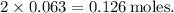
To find the mass of silver produced, we use the formula:
 , giving us
, giving us
 .
.
However, since not all the silver oxide is converted to silver, we must consider the limiting reactant. The limiting reactant is Ag₂O, and thus, the mass of silver produced is