Question

Determine the maximum normal stress developed in the bar when it is subjected to a tension of p = 2 kip?

Answer 1

The maximum normal stress developed in the bar when it is subjected to a tension of 2 kip is approximately 4,533,551.07 N/m².

Step-by-step explanation:

To determine the maximum normal stress developed in the bar, we first need to calculate the cross-sectional area of the bar. The formula for the cross-sectional area of a cylinder is

`A = πr^2`

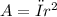
r is the radius of the cylinder. In this case, the diameter of the bar is given as 5.0 cm, so the radius is half of that, which is 2.5 cm or 0.025 m. Plugging this value into the formula, we get

`A = π(0.025)^2 = 0.0019635 m^2`

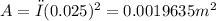
Next, we can use the formula for stress, which is stress = force / area. The tension applied to the bar is given as 2 kip, which is equivalent to 2000 lb or 8896.44 N. Plugging this value into the formula, we get stress = 8896.44 N / 0.0019635 m^2 = 4,533,551.07 N/m².

Therefore, the maximum normal stress developed in the bar when it is subjected to a tension of 2 kip is approximately 4,533,551.07 N/m².