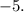The consecutive negative integers are -5 and -4. Their product, -5 * -4, equals 20. Therefore, the value of the lesser integer is -5.
Let the consecutive negative integers be \( x \) and \( (x-1) \). According to the problem, their product is 20, so we can set up the equation:
![\[ x \cdot (x-1) = 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nboyzt0zs0ckg7yzc59spkscir9qw3gm3z.png)
Expanding and rearranging the equation gives us a quadratic equation:
![\[ x^2 - x - 20 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v0stexbnzpxf6wdzcsl6ntsuyjhcavh8e5.png)
Now, we can factor the quadratic equation:
![\[ (x-5)(x+4) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ipnd3hn2y1019733tg4apbvlsepyiarl7u.png)
This implies that either
 Solving these equations gives us two possible values for
Solving these equations gives us two possible values for
 Since we're dealing with negative integers, we discard the positive solution, leaving us with
Since we're dealing with negative integers, we discard the positive solution, leaving us with

Therefore, the consecutive negative integers are
 and
and
 , and the lesser integer is
, and the lesser integer is
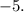 So, the answer to the problem is that the value of the lesser integer is
So, the answer to the problem is that the value of the lesser integer is