Final Answer:
The centroid
 for the beam's cross-sectional area is the geometric center of the shape.
for the beam's cross-sectional area is the geometric center of the shape.
Step-by-step explanation:
The centroid
 of a beam's cross-sectional area is the point where the entire area can be considered to be concentrated. For simple and symmetric shapes, such as rectangles or circles, the centroid is at the center of the shape. This is the case when the shape has uniform density or material distribution.
of a beam's cross-sectional area is the point where the entire area can be considered to be concentrated. For simple and symmetric shapes, such as rectangles or circles, the centroid is at the center of the shape. This is the case when the shape has uniform density or material distribution.
In more complex cases, where the beam's cross-section is irregular or consists of multiple shapes, the centroid is found by calculating the weighted average of the individual centroids of each sub-area. Mathematically, the centroid
 is given by the sum of the products of each sub-area's centroid
is given by the sum of the products of each sub-area's centroid
 and its corresponding area
and its corresponding area
 divided by the total area
divided by the total area
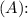
![\[ \bar{y} = (\sum (A_i \cdot y_i))/(\sum A_i) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kde016negfc2q2r7iij4v97h5dfjcg886v.png)
Here,
 represents the centroid,
represents the centroid,
 is the area of each sub-section, and
is the area of each sub-section, and
 is the distance from the reference axis to the centroid of each sub-area. This formula accounts for the distribution of material within the cross-section.
is the distance from the reference axis to the centroid of each sub-area. This formula accounts for the distribution of material within the cross-section.
In conclusion, finding the centroid is crucial for structural analysis as it helps determine the point through which the resultant force of the entire cross-sectional area can be considered to act, simplifying calculations for various engineering applications.