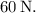1. Free Body Diagram (FBD):
- Tension (T) horizontally.
- Weight (mg) vertically.
2. Angular Velocity (
 ):
):
-
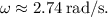
3. Acceleration (a):
-

4. Period (T):
-
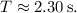
5. Tension with Increased Radius (
 ):
):
-
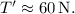
6. Tension with Doubled Angular Velocity (
 ):
):
-
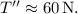
Let's break down the problem step by step:
a.) Free Body Diagram (FBD) of the puck:
The puck is undergoing circular motion, so there must be a centripetal force acting towards the center. The only horizontal force is the tension in the rope. The weight (mg) acts vertically downward.
### b.) Angular velocity (
 ):
):
The centripetal force (Fc) is provided by the tension in the rope:
![\[ F_c = T \]](https://img.qammunity.org/2024/formulas/physics/high-school/16a6xl1ukmcsfk800os4d41okww5b201ax.png)
The centripetal force is also given by the formula
 , where v is the tangential velocity. In uniform circular motion,
, where v is the tangential velocity. In uniform circular motion,
 . Setting these two equations equal to each other:
. Setting these two equations equal to each other:
![\[ T = (m(\omega r)^2)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ja29rv10srs37unzdfpb4hos8b52q5qi5l.png)
Solving for

![\[ \omega = \sqrt{(T)/(m)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/60zywnaxxahaeopytthibht1onlpaymkbu.png)
Substitute the given values:
![\[ \omega = \sqrt{\frac{15 \, \text{N}}{2 \, \text{kg}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/dsiyl89en2b3z4umv1obwmdhko3jflcpuw.png)
![\[ \omega \approx 2.74 \, \text{rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/qq5lfoyc224p56ufmnnjrw1wxilh9u1fou.png)
### c.) Acceleration (a):
The centripetal acceleration (
 ) is given by
) is given by
 , where v is the tangential velocity. In uniform circular motion,
, where v is the tangential velocity. In uniform circular motion,
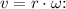
![\[ a_c = ((r \cdot \omega)^2)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/eto1wxa7a0bcx9k462bloexnh8yitu7p52.png)
Substitute the values:
![\[ a_c = \frac{(0.80 \, \text{m} \cdot 2.74 \, \text{rad/s})^2}{0.80 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/36skjw33z38tfdr4u2rqml8vptns5ufq8g.png)
![\[ a_c \approx 8.9375 \, \text{m/s}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/oyjrh1mswry854l0n9hl4lf2gddgq21k7r.png)
### d.) Period (T):
The period is the time it takes for one complete revolution, and it's related to angular velocity (
 ) by the formula
) by the formula
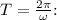
![\[ T = \frac{2\pi}{2.74 \, \text{rad/s}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/5h6l8waijgd5lurkw3x1klb6mw00r5nhj6.png)
![\[ T \approx 2.30 \, \text{s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/6jvzti2g51xlkx12tznrz1w0nhunx8x7ge.png)
e.) Tension with increased radius (
 ):
):
Using the centripetal force formula (
 ) and the fact that
) and the fact that
 , we can write the tension as:
, we can write the tension as:
![\[ T = (m(\omega r)^2)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ja29rv10srs37unzdfpb4hos8b52q5qi5l.png)
Since
 is constant:
is constant:
![\[ T' = (m(\omega r')^2)/(r') \]](https://img.qammunity.org/2024/formulas/physics/high-school/cbqitm37knotk5oc6tc5ty0dejp78af49d.png)
![\[ T' = \frac{m(\omega \cdot 1.60 \, \text{m})^2}{1.60 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/j0mtj0s75i73svcj7cvehd6yubnv6ngwp0.png)
![\[ T' \approx 60 \, \text{N} \]](https://img.qammunity.org/2024/formulas/physics/high-school/cxyrcjwsrt3p6f91kx2m6zfnwvdc7mfg5d.png)
f.) Tension with doubled angular velocity (
 ):
):
![\[ T'' = (m(\omega' r)^2)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/tfja9rlp5guso5azcz7e36ja2shm6ystpl.png)
![\[ T'' = \frac{m((2 \cdot \omega) \cdot 0.80 \, \text{m})^2}{0.80 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/9l6kteqfdldzxm6t7wdz7wqtbvmrp5vu1k.png)
![\[ T'' \approx 60 \, \text{N} \]](https://img.qammunity.org/2024/formulas/physics/high-school/yh4hr05achuofwev7hsd36qxicq278iofx.png)
In both cases (increased radius and doubled angular velocity), the tension in the rope remains approximately