Question

Kenna invests $5,000 today, compounded monthly, with an annual interest rate of 8.52%. What amount of interest will she earn in one year?

Answer 1

Kenna will earn approximately $426 in interest in one year.

Step-by-step explanation:

When calculating compound interest, the formula
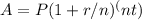`A = P(1 + r/n)^(nt)` is used, where:

- A is the future value of the investment/loan, including interest.

- P is the principal investment amount (the initial deposit or loan amount).

- r is the annual interest rate (decimal).

- n is the number of times that interest is compounded per year.

- t is the number of years the money is invested or borrowed.

In this case, Kenna's principal (P) is $5,000, the annual interest rate (r) is 8.52% (or 0.0852 as a decimal), and the interest is compounded monthly (n = 12 times per year). The time (t) is one year.

Using the formula, we can calculate the future value of the investment after one year. The interest earned is the difference between the future value and the initial principal.

Therefore, Kenna's future value (A) after one year is given by:

`\[ A = 5000 * (1 + 0.0852/12)^(12 * 1) \]`

After calculating A, the interest earned is obtained by subtracting the initial principal:

`\[ \text{Interest} = A - P \]`

Solving these equations, we find that Kenna will earn approximately $426 in interest in one year. This is the amount her initial investment will grow due to the compounding effect of the monthly interest rate over the course of the year.