Question

Find the area of equilateral triangle with side a. Please answer with completely simplified exact values. Answer: A = sq. Units

Answer 1

It is given that the length of a side of a triangle is given by 'a'.

It is an equilateral triangle.

So the three sides will be of equal length and is a, a, a units.

Now the semi perimeter of the equilateral triangle is given by :

`$S=(a+a+a)/(2)$`

`$=(3)/(2)a$`

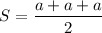
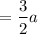
Therefore, using the Heron's formula, we can find the area of the equilateral triangle.

Area of the equilateral triangle is given by :

`$A =√(S(S-a)(S-a)(S-a))$`

`$A =\sqrt{(3a)/(2)\left((3a)/(2)-a\right)\left((3a)/(2)-a\right)\left((3a)/(2)-a\right)}$`

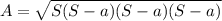
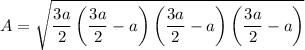
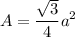`$A=(\sqrt3)/(4)a^2$` square units.