Question

A stone is thrown vertically upwards with an initial velocity of 29.4m/s from the top tower,34.3m high. Find

1: time taken to reach maximum height
2: total time which elapses before it reaches the ground​
I need urgent help please

Answer 1

2s [seconds], 6s [seconds]

Step-by-step explanation:

Using the equations of Motion :-

`v = u + at`

`s = ut + (1)/(2) a {t}^(2)`

`{v}^(2) = {u}^(2) + 2as`

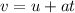
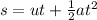
We pick our best formula for our need

--

NOTE:: ACCELERATION (A) = GRAVITY = 9.8 MS-2 OR 49/5 MS-2

NOTE:: ''•''MEANS MULTIPLICATION AND ''^'' MEANS POWER OF..

NOTE:: TRANSPOSE MEANS TO SWITCH SIDES IN LINEAR EQUATION & + goes -, - goes + etc

--

Inital Velocity (u) = 29.4 ms-1

Displacement (s) = 34.3m

--

1)

• v = u + at OR v = u + gt
• v [velocity not given] = 0, u = 29.4, g = -9.8 [approx on earth {negative because gravity is pulling down}] and we need to find t
• 0 + 29.4 + -9.8 • t
• 0 + 29.4 + -9.8t [transpose -9.8t]
• 9.8t = 29.4
• t = 29.4/9.8
• t = 3
• 3s

.. 3s [seconds]

2)

• s = ut+1/2at^2 OR s = ut + 1/2gt^2
• s [displacement is 0m as when it reaches ground level, displacement/height would be 0m] = 0m, g = -9.8 ms-2, u = 29.4 ms-1, and we need to find t
• 0 = 29.4 • t + 1/2 • -9.8 • t^2
• 0 = 29.4t + (-9.8t^2)/2 [transpose (-9.8t^2)/2 and solve (-9.8t^2)/2]
• 4.9t^2 = 29.4t
• t^2 = (29.4t)/4.9
• t^2 = 6t
• (t^2)/t = 6 • t/t
• t = 6
• 6s

.. 6s [seconds]