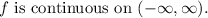Finall Answer:
The function
 is continuous on
is continuous on

Step-by-step explanation:
For the function
 limits from both sides of the function must be equal.
limits from both sides of the function must be equal.
For
 continuity at
continuity at
 these two limits must be equal, so
these two limits must be equal, so
 - 5c \). Solving this equation yields
- 5c \). Solving this equation yields
 which ensures the function
which ensures the function