Question

Evaluate the integral using integration by parts with the indicated choices of u and dv. (Use c for the constant of integration.)

1) x²e⁹x + ce⁹x
2) xe⁹x - 9e⁹x + c
3) xe⁹x + 9e⁹x + c
4) x²e⁹x - 9e⁹x + c

Answer 1

To evaluate the integral using integration by parts, choose
`u = x^2` and
`dv = e^9x dx`. Apply the integration by parts formula to find the integral step-by-step.

Step-by-step explanation:

To evaluate the given integral using integration by parts, we need to choose u and dv.

Let
`u = x^2` and
`dv = e^9x dx`.

Then, du = 2x dx and
`v = (1/9)e^9x`.

Using the integration by parts formula:

`\int {u} \, dv = uv -\int {v} \, du`

`\int\ {x^2e^9x} \, dx = (x^2)(1/9)e^9x - \int\ {(1/9)e^9x(2x)} \, dx`

=
`(1/9)x^2e^9x - (2/9)\int\ {x^2e^9x} \, dx`

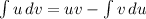
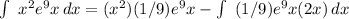
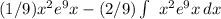
Now we have a similar integral as the one we started with. We can repeat the process of integration by parts to evaluate the remaining integral.

So, the correct choice is option 4)
`x^2e^9x - 9e^9x + c`