Question

Find the angle between the line x = 1 – t, y = 3t, z = 1 t and the plane 2x – y - 3z = 6?

Answer 1

To find the angle between the given line and plane, calculate the dot product and magnitudes of the line's direction vector and plane's normal vector, then use the cosine formula to determine the angle.

Step-by-step explanation:

To find the angle between a line and a plane, we need to determine the angle between the line's direction vector and the plane's normal vector. The direction vector of the line x = 1 − t, y = 3t, z = 1 + t can be given as D = − 1, 3, 1. The normal vector of the plane 2x − y − 3z = 6 is N = 2, − 1, − 3. To find the angle θ between D and N, we use the formula cos(θ) = (D · N) / (|D| |N|), where · denotes the dot product and | | is the magnitude.

First, compute the dot product D · N:

• D · N = (− 1)(2) + (3)(− 1) + (1)(− 3) = − 2 − 3 − 3 = − 8

Next, calculate the magnitudes of D and N:

• 
  `|D| = √((− 1)^2 + 3^2 + 1^2) = √(1 + 9 + 1) = √11|N| = √(2^2 + (− 1)^2 + (− 3)^2) = √(4 + 1 + 9) = √14`

Now find cos(θ):

• cos(θ) = (− 8) / (√11 × √14)
• 
  `θ = cos^(− 1)((− 8) / (√11 × √14))`

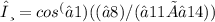
Use a calculator to find θ, which gives the angle between the line and plane.