Question

Find the volume V of the solid obtained by rotating the region bounded by the curves y = 7x and y = 7x about the line y = 7.

Answer 1

To find the volume V of the solid obtained by rotating the region bounded by the curves y = 7x and y = 7x about the line y = 7, you can use the disk method. The volume V is
`\((98)/(3)` π cubic units.

Step-by-step explanation:

To find the volume V of the solid obtained by rotating the region bounded by the curves y = 7x and y = 7x about the line y = 7, you can use the disk method.

The curves y = 7x and y = 7x intersect at x = 1, where y = 7(1) = 7.

Now, for each x between 0 and 1, the outer radius is 7 (the distance from the axis of rotation to the curve y = 7x, and the inner radius is 7 (the distance from the axis of rotation to the curve y = 7x.

The volume of each disk is given by:

`\[ V_{\text{disk}}` = π · Outer Radius² - Inner Radius²

Substitute the values:

`\[ V_{\text{disk}}` = \pi(7^2 - (7x)^2) \]

Now, integrate to find the total volume:

V =
`\int_(0)^(1)` π (7² - (7x)² dx

V = π
`\int_(0)^(1)` (49 - 49x²) dx

V = π [ 49x -
`(49)/(3)x^3 ]_(0)^(1)`

V = π ( 49 -
`(49)/(3)` )

V = π
`\left( (98)/(3) \right)`

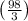
So, the volume V is
`\((98)/(3)` π cubic units.