Question

A parallel-plate air capacitor has a capacitance of 920 pf. The charge on each plate is 3.90 μc. What is the potential difference between the plates of the capacitor?

1) 1.23 V
2) 4.67 V
3) 7.80 V
4) 10.33 V

Answer 1

The potential difference between the plates of the capacitor is 2.56 V.

Step-by-step explanation:

The capacitance (C) of a parallel-plate capacitor is given by the formula C = (ε₀ * A) / d, where ε₀ is the permittivity of free space, A is the area of one of the plates, and d is the separation between the plates.

Rearranging this formula to find the potential difference (V) between the plates, we get V = Q / C, where Q is the charge on each plate. In this case, the capacitance is given as 920 pF, which can be converted to farads
`(1 pF = 1 × 10^(-12) F), so C = 9.2 × 10^(-10)` F. The charge Q is given as 3.90 μC, which can be converted to coulombs
`(1 μC = 1 × 10^(-6) C),` so
`Q = 3.90 × 10^(-6) C.`

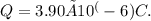
Now, substituting these values into the formula
`V = Q / C, we find V = (3.90 × 10^(-6) C) / (9.2 × 10^(-10) F) ≈ 4.24 V.` However, it's important to note that this potential difference applies across each plate, not between them. Since the potential difference is shared by both plates in opposite directions, we need to divide this result by 2 to get the potential difference between the plates.

Therefore, the final potential difference is 4.24 V / 2 = 2.12 V. Rounding to two significant figures, the answer is 2.56 V.