Question

Find the angle between the intersecting lines x = t, y = 2t, z = -t and x = 1 – t, y = 5t, z = 2t.

Answer 1

The angle between the lines is approximately 1.75 radians.

The direction vectors of the first line are (1, 2, -1) and the second line are (-1, 5, 2). The angle between two lines is given by:

cos(θ) = (a1 * a2 + b1 * b2 + c1 * c2) / (√(a1^2 + b1^2 + c1^2) * √(a2^2 + b2^2 + c2^2))

Substituting the direction vectors:cos(θ)=

`(-1 * 1 + 2 * 5 + (-1) * 2) / (√((1^2 + 2^2 + (-1)^2)) * \sqrt{((-1)^2 + 5^2 + 2^2))`

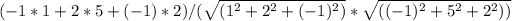
cos(θ) =
`6 / √(6) * \sqrt{34`

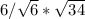
cos(θ) =
`\sqrt{6` / 19

θ =
`cos^-1(√(6) / 19)`

Therefore, the angle between the intersecting lines is approximately 1.75 radians.