Answer:
The probability that the mean daily precipitation will be 0.11 inches or less for a random sample of November days
P(X≤ 0.11) = 0.4404
Explanation:
Step(i):-
Given that the mean of the Population = 0.10 inches
Given that the standard deviation of the population = 0.07inches
Let 'X' be a random variable in a normal distribution
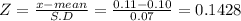
Step(ii):-
The probability that the mean daily precipitation will be 0.11 inches or less for a random sample of November days
P(X≤ 0.11) = P(Z≤0.1428)
= 1-P(Z≥0.1428)
= 1 - ( 0.5 +A(0.1428)
= 0.5 - A(0.1428)
= 0.5 -0.0596
= 0.4404
Final answer:-
The probability that the mean daily precipitation will be 0.11 inches or less for a random sample of November days
P(X≤ 0.11) = 0.4404