Explanation:
We got
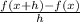
The function here is
9x^2 so we got now
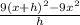
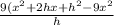
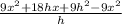
Cancel out terms.
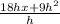
If we direct subsitue we get
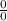
which is intermidate form in calculus so now, let try to find another way to evaluate this, we can factor out 9h
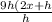
Cancel out h
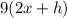
Subsitue 0 for h.
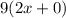
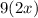
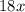
The answer here is 18x.
Congrats. We just found the derivative of a function.