Question

The given function is \( C(t)=C_{0}(1+r)^{t} \), where: - \( C(t) \) is the cost of the product after \( t \) years, - \( C_{0} \) is the initial cost of the product, - \( r \) is the rate of inflation, and - \( t \) is the time in years. We are given that \( C_{0} = \$220 \), \( r = 3.5\% = 0.035 \) (converted from percentage to decimal), and \( t = 5 \) years. We need to find \( C(t) \), the cost of the airline ticket after 5 years. Substitute the given values into the function: \[ C(t) = C_{0}(1+r)^{t} \] \[ C(5) = 220(1+0.035)^{5} \] Now, calculate the value: \[ C(5) = 220(1.035)^{5} \] \[ C(5) = 220 * 1.18769 \] (rounded to five decimal places) Finally, round the result to two decimal places: \[ C(5) = \$261.29 \] So, the inflation-adjusted cost of a $220 airline ticket in 5 years will be approximately **\$261.29**.

Answer 1

The population, according to the exponential function P(t) = P₀
`e^{(rt)` with P₀ = 500, r = 0.02, and t = 10 years, is approximately 611 when rounded to the nearest whole number.

In the given exponential function P(t) = P₀
`e^{(rt)`, where P(t) is the population after t years, P₀ is the initial population, r is the growth rate, and t is the time in years, we are provided with P₀ = 500, r = 0.02, and t = 10.

Substitute these values into the formula:

P(10) = 500
`e^((0.02 * 10))`

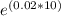
Calculate the exponent:

P(10) = 500
`e^{0.2`

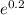
Evaluate the exponential expression:

P(10) = 500 * 1.22140

Round the result to the nearest whole number:

P(10) = 611

Therefore, the population after 10 years, rounded to the nearest whole number, is 611. The exponential function illustrates the growth of the population over time under the given growth rate and initial population conditions.

Complete question:

Given the exponential function P(t) = P₀
`e^{(rt)`, where:

P(t) is the population after t years,

P₀ is the initial population,

r is the growth rate, and

t is the time in years.

If P₀ = 500, r = 0.02, and t = 10, what is the population after 10 years? Calculate and round your answer to the nearest whole number.