Answer:
See Below.
Explanation:
Please refer to the attachment below.
In order to complete the proof, we create a new segment DE that extends from D and is equal to AD. The endpoint of DE will be connected to B.
Statements: Reasons:
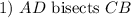 Given
Given
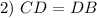 Definition of Bisector
Definition of Bisector
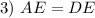 Given
Given
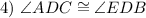 Vertical Angles are Congruent
Vertical Angles are Congruent
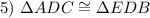 SAS Congruence
SAS Congruence
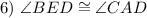 CPCTC
CPCTC
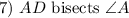 Given
Given
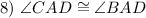 Definition of Congruence
Definition of Congruence
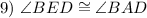 Substitute
Substitute
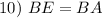 Isosceles Triangle Theorem
Isosceles Triangle Theorem
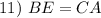 CPCTC
CPCTC
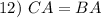 Substitute
Substitute
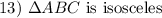 Isosceles Triangle Definition
Isosceles Triangle Definition