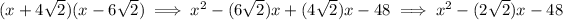Question

quadratic equation x²-√2x-12 has zeroes as α and β. Now forma quadratic equation whos zeroes are 2α and 2β

Answer 1

`\text{Standard Form: }x^2 - (2√(2))x - 48\\\text{Factored Form: }(x+4√(2))(x-6√(2))`

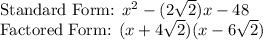
Explanation:

We're given the equation:
`x^2 - (√(2))x - 12`

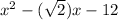
We can find the zeroes of this function by using the quadratic formula defined as:
`x=(-b\pm √(b^2 - 4ac))/(2a)`

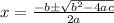
In this case:
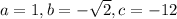`a=1,b=-√(2), c=-12`. So if we substitute these values in we get the following:

`x=\frac{-(-√(2))\pm \sqrt{(-√(2))^2 - 4(1)(-12)}}{2(1)}\\\\x=(√(2) \pm √(2 + 48))/(2)\\\\x=(√(2) + √(50))/(2)\\\\x = (√(2) \pm √(25) * √(2))/(2)\\\\x = (√(2) \pm 5√(2))/(2)`

So from here we'll get our two zeroes, but you may notice, regardless of whether we pick the positive or negative square root, the denominator is two. So if we're looking for an equation with
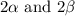`2\alpha \text{ and }2\beta` we just multiply this by two to get:

`x = √(2) \pm 5√(2)`

Now from here let's find both solutions. First let's take the positive square root to get:
`x = √(2) + 5√(2) \implies 6√(2)`

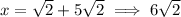
If we take the negative square root we get:
`x = √(2) - 5√(2)\implies -4√(2)`

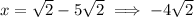
So now that we have the two zeroes, let's start forming our quadratic equation. In this case it's really useful to start with factored form. In this form we express a quadratic or generally any polynomials in terms of its factors.

The factored form of quadratic looks something like this:
`f(x)=a(x-b)(x-c)`

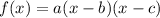
where b and c are zeroes and a is some value that determines the stretch/compression of the quadratic.

The "a" value doesn't change the zeroes, so for simplicity let's just say, that a=1 in this case. This gives us the quadratic:
`(x-(-4√(2)))(x-6√(2))\implies (x+4√(2))(x-6√(2))`

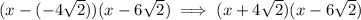
We can leave it in this factored form, but we can also expand this using FOIL to express it in standard form.

`(x + 4√(2))(x-6√(2))\implies x^2 - (6√(2))x + (4√(2))x - 48\implies x^2 - (2√(2))x - 48`