Answer:
secant function:
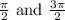
cosecant function:
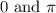
Explanation:
the cosecant and secant functions can be defined as the reciprocals of the sin and cos function in their respective order.
This just means that the following is true:
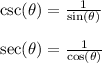
You may notice that the sin and cos functions are in the denominator. You also may know that we cannot divide by zero. So to find what angles are not in the domain, we simply look for when the denominator is zero, since it won't be defined at that angle.
So let's start with the cosecant function. We of course know that:
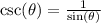
so from here, we want to find when the following is true:
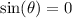
We can use the unit circle to find when this is true on the interval
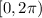
I attached an image for reference, and we can attribute the sin function to the y-value, and the y-value is only equal to zero when the angle is at 0 and
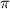
So the angles 0 and
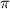 are not in the domain of the cosecant function
are not in the domain of the cosecant function
Now let's look at the cosecant function which can be defined as:
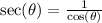
From here, we need to look for when the following is true:
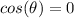
We can refer to the unit circle once again, but unlike the sin function, the cos function corresponds to the x-value, and looking at the unit circle this is only equal to zero at the following angles:
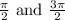
So these angles are not included in the domain ot the secant function.