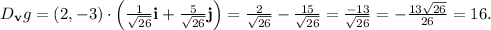Final Answer:
The directional derivative of the function
 at the point (1, 1) in the direction of the vector
at the point (1, 1) in the direction of the vector
 is 16.
is 16.
Step-by-step explanation:
The directional derivative represents the rate of change of a function in a specific direction. To compute it at the point (1, 1) in the direction of the vector
 , start by finding the gradient of the function g(p, q). The gradient of g is
, start by finding the gradient of the function g(p, q). The gradient of g is
 .
.
Next, evaluate the gradient at the point (1, 1):
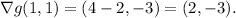
The directional derivative
 in the direction of
in the direction of
 is calculated by taking the dot product of the gradient of g at the point with the unit vector in the direction of
is calculated by taking the dot product of the gradient of g at the point with the unit vector in the direction of
 :
:
 .
.
The given vector
 has a magnitude of
has a magnitude of
 . The unit vector in the direction of
. The unit vector in the direction of
 is
is
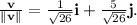
Finally, compute the directional derivative: