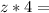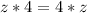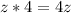Answer:
Step 1:
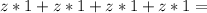
Step 2:
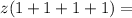
Step 3:
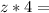
Step 4:
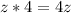
Explanation:
Given
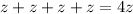
Required
Match the steps with equivalent properties
Step 1: Multiplicative Identity Property
This states that:
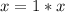
So, the expression becomes:
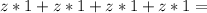
Step 2: Distributive Property
This states that:
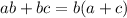
So, the expression becomes
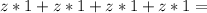
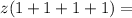
Step 3: Addition
Here, we simply add the expressions in the bracket
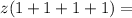
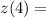
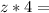
Step 4: Commutative Property of Multiplication
This states that:
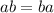
So, we have: