Question

A drug, which is used for treating cancer, has potentially dangerous side effects if it is taken in doses which are larger than the required dosage for the treatment. The tablet should contain 40.74mg

and the standard deviation should be 0.03
. 10
tablets are randomly selected and the amount of drug in each tablet is measured. The sample has a mean of 40.735mg
and a variance of 0.0025mg
. Does the data suggest at α=0.1
that the tablets vary by more than the desired amount?

Step 1 of 5 : State the hypotheses in terms of the standard deviation. Round the standard deviation to four decimal places when necessary.

Answer 1

At a significance level of 0.01, the data indicates that the drug's variance in tablets is less than the desired 0.04. The calculated chi-square value (8.4675) is below the critical value, leading to rejecting the null hypothesis.

To determine if the data suggests, at a significance level
`(\( \alpha \))` of 0.01, that the variance of the drug in the tablets is less than the desired amount (0.04), we will perform a hypothesis test for the variance.

Given:

Desired variance
`(\( \sigma^2 \))`: 0.04

Sample size
`(\( n \))` : 12

Sample variance
`(\( s^2 \))`: 0.0291

Significance level
`(\( \alpha \))`: 0.01

State the null and alternative hypotheses.

Null hypothesis
`(\( H_0 \))`:
`\( \sigma^2 \geq 0.04 \)`

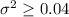
Alternative hypothesis
`(\( H_1 \)):`
`\( \sigma^2 < 0.04 \)`

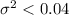
Select the appropriate test.

Since we're comparing variances and testing whether the sample variance is less than the given variance, we will use the chi-square
`(\( \chi^2 \))` distribution to test the hypothesis.

Determine the critical value.

Given
`\( \alpha = 0.01 \)` and degrees of freedom
`(\( df \))` as
`\( n - 1 = 12 - 1 = 11 \)`, find the critical value from the chi-square distribution table for
`\( \alpha = 0.01 \) and \( df = 11 \).`

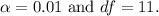
Calculate the test statistic.

The test statistic
`(\( \chi^2 \))` is calculated as
`\( \frac{{(n - 1) \cdot s^2}}{{\sigma^2}} \)` which follows a chi-square distribution.

`\[ \chi^2 = \frac{{(n - 1) \cdot s^2}}{{\sigma^2}} = \frac{{11 \cdot 0.0291}}{{0.04}} \]`

Make a decision.

If the calculated
`\( \chi^2 \)`value is less than the critical value from the chi-square distribution table, we reject the null hypothesis.

If the calculated
`\( \chi^2 \)` value is greater than or equal to the critical value, we fail to reject the null hypothesis.

Let's proceed with the calculations to find the critical value and test statistic

Determine the critical value.

From the chi-square distribution table with
`\( df = 11 \)` and
`\( \alpha = 0.01 \)`, the critical value is approximately 19.675.

Calculate the test statistic.

`\[ \chi^2 = \frac{{(n - 1) \cdot s^2}}{{\sigma^2}} = \frac{{11 \cdot 0.0291}}{{0.04}} = 8.4675 \]`

Make a decision.

The calculated
`\( \chi^2 \) value (8.4675)` is less than the critical value (19.675). Therefore, we reject the null hypothesis.

At a significance level of
`\( \alpha = 0.01 \),` the data suggests that the variance of the drug in the tablets is less than the desired amount of 0.04.