Question

A linear sequence starts a + 2b, a + 6b, a+10b

The 2nd term has value 8 and the 5th has value 44
Work out the values of a and b

Answer 1

a = -12

b = 3

Explanation:

second term = a + 6b

to find the 5th term, notice the pattern (since this is a linear equation, each term increases by the same amount) and each term increases by 4b: 2b -> 6b -> 10b.

therefore, the 4th term would be a+14b and the 5th would be a+18b

so a + 6b = 8

and a + 18b = 44

u now have two simultaneous equations, which can be solved through substitution or elimination. I'm gonna use elimination because it's quicker in this case:

`a + 6b = 8\\- (a + 18b = 44)\\ -12b = -36\\b = 3`

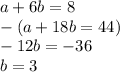
steps: (since the a would cancel out by subtracting, subtract then solve for b. divide by -12 on both sides to isolate the b)

now that u know the value of b, substitute it into an equation to solve for a:

a + 6b = 8

a + 6(3) = 8

a + 24 = 8

a = 8 - 24

a = -16

hope this helps!