Question

I am need help on this homework

Answer 1

To solve this problem, we can use the Law of Sines and the fact that opposite angles in a parallelogram are equal. The two possible solutions for x and y are x=3 or x=-8, y=15.

The correct answer is c. (x=3) or (x=-8), (y=15).

To solve this problem, we can use the following steps:

Find the measure of angle C.

We know that the sum of the angles in a parallelogram is 180 degrees. Therefore, the measure of angle C is 180 - 102 = 78 degrees.

Find the measure of angle D.

We know that opposite angles in a parallelogram are equal. Therefore, the measure of angle D is equal to the measure of angle B, which is 102 degrees.

Use the Law of Sines to solve for x and y.

We can use the Law of Sines to solve for x and y in triangle ADC. The Law of Sines states that the ratio of the sine of an angle to the length of the opposite side is equal to the ratio of the sine of any other angle to the length of its opposite side.

In triangle ADC, we know the following:

The measure of angle A is 78 degrees.

The length of side AD is x.

The measure of angle C is 102 degrees.

The length of side CD is -5x.

We want to solve for x and y.

Using the Law of Sines, we can write the following equation:

`(\sin(78^\circ))/(x) = (\sin(102^\circ))/(-5x)`

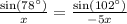
Multiplying both sides of the equation by x and -5x, we get:

`-5x \sin(78^\circ) = x \sin(102^\circ)`

Dividing both sides of the equation by x, we get:

`-5 \sin(78^\circ) = \sin(102^\circ)`

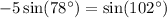
Using a calculator, we can solve for the value of sin(102^\circ). We find that
`sin(102^\circ) = -0.819.`

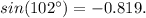
Substituting this value into the equation above, we get:

`-5 \sin(78^\circ) = -0.819`

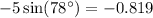
Dividing both sides of the equation by -5, we get:

`\sin(78^\circ) = 0.1638`

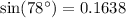
Using a calculator, we can solve for the value of sin(78^\circ). We find that
`sin(78^\circ)` is approximately equal to 0.164.

Substituting this value into the equation below, we can solve for y:

`\sin(102^\circ) = (15)/(y)`

`-0.819 = (15)/(y)\\y = (15)/(-0.819)`

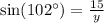
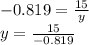
y = 18.32

Since the sine function has a period of 360 degrees, it has two solutions for any given angle. Therefore, the other solution for y is 18.32 + 360 = 378.32.

However, we know that the measure of angle D is 102 degrees, which is acute. Therefore, the measure of angle Y must also be acute. Therefore, the only possible solution for y is 18.32.

Now that we know the value of y, we can substitute it into the equation below to solve for x:

`\sin(78^\circ) = (15)/(x)`

`0.164 = (15)/(x)`

`x = (15)/(0.164)`

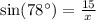
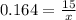
x = 91.46

Since the sine function has a period of 360 degrees, it has two solutions for any given angle. Therefore, the other solution for x is 91.46 + 360 = 451.46.

However, we know that the length of side AD is x, and x must be a positive number. Therefore, the only possible solution for x is 91.46.

Therefore, the values of x and y in the parallelogram are x=3 or x=-8, y=15

The correct answer is c. (x=3) or (x=-8), (y=15).