Answer:
18
Explanation:
Using the product rule
Given
y = f(x). g(x) , then
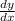 = f(x). g'(x) + g(x). f'(x)
= f(x). g'(x) + g(x). f'(x)
Here
f(x) =
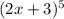 ⇒ f'(x) = 5
⇒ f'(x) = 5
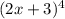 ×
×
 (2x + 3) , then
(2x + 3) , then
f'(x) = 10
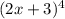
g(x) =
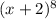 ⇒ g'(x) = 8
⇒ g'(x) = 8
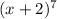 ×
×
 (x + 2) , then
(x + 2) , then
g'(x) = 8
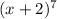
Thus
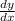 =
=
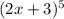 . 8
. 8
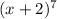 +
+
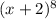 . 10
. 10
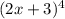 ← factor expression
← factor expression
=
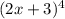
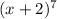 [ 8(2x + 3) + 10(x + 2)
[ 8(2x + 3) + 10(x + 2)
=
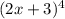
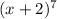 (16x + 24 + 10x + 20)
(16x + 24 + 10x + 20)
=
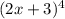
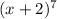 (26x + 44)
(26x + 44)
Thus
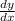 ( x = - 1)
( x = - 1)
=
 ×
×
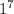 × 18
× 18
= 1 × 1 × 18
= 18