Question

1.

Use the Rydberg equation to calculate the energy (in J) and then find the wavelength
in (nm) for the following transitions.
-18
AE = 2.179x10
a.
3-2.

Answer 1

Approximately
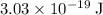`3.03* 10^(-19)\; \rm J`, which corresponds to a wavelength of approximately
`6.56 * 10^(2)\; \rm nm` in vacuum.

Step-by-step explanation:

When the electron of a hydrogen atom transits from energy level
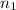`n_1` to
`n_2`, the energy change would be:

`\displaystyle \Delta E \approx 2.179 * 10^(-18)\; {\rm J} \, \left(\frac{1}{{(n_1)}^(2)} - \frac{1}{{(n_2)}^(2)}\right)`.

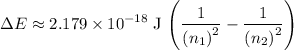For the transition from
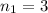`n_1 =3` to
`n_2 = 2`:

`\begin{aligned}\Delta E &\approx 2.179 * 10^(-18)\; {\rm J} \, \left(\frac{1}{{(n_1)}^(2)} - \frac{1}{{(n_2)}^(2)}\right)\\ &= 2.179 * 10^(-18)\; {\rm J} \, \left(\frac{1}{{3}^(2)} - \frac{1}{{2}^(2)}\right) \\ &\approx -3.02639 * 10^(-19) \; \rm J \\ &\approx -3.03* 10^(-19)\; \rm J\end{aligned}`.

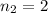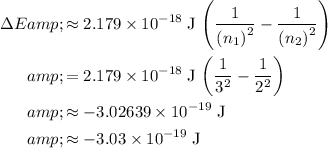The value of
`\Delta E` is negative because energy is released during this transition.

Look up Planck's Constant (for finding frequency from energy) and the speed of light in vacuum (for finding wavelength from frequency.)

• Planck's Constant:
  `h \approx 6.62607 * 10^(-34) \; \rm J \cdot s^(-1)`.
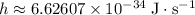• Speed of light in vacuum:
  `c \approx 2.99792 * 10^(8)\; \rm m \cdot s^(-1)`.

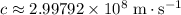Calculate the frequency
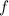`f` of photons from this transition using the Planck-Einstein relation:

`E = h \cdot f`.

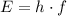Therefore:

`\begin{aligned}f &= (E)/(h)\end{aligned}`.

Calculate the wavelength
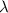`\lambda` of these photos in vacuum:

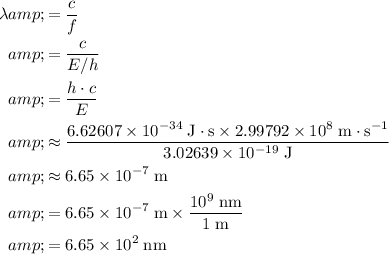`\begin{aligned}\lambda &= (c)/(f) \\ &= (c)/( E/ h) \\ &= (h \cdot c)/(E) \\ &\approx (6.62607 * 10^(-34)\; \rm J \cdot s * 2.99792 * 10^(8)\; \rm m \cdot s^(-1))/(3.02639 * 10^(-19)\; \rm J) \\ &\approx 6.65 * 10^(-7)\; \rm m \\ &= 6.65 * 10^(-7)\; \rm m * (10^(9)\;\rm nm)/(1\; \rm m) \\ &= 6.65 * 10^(2)\; \rm nm\end{aligned}`.