Question

-Q/7 greater or equal to -1

Answer 1

The solution:
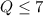`\(Q \leq 7\)`. Represents values making
`\(-(Q)/(7) \geq -1\)` true, including 7, on a number line.

To solve the inequality
`\(-(Q)/(7) \geq -1\)`, we'll use basic algebraic steps to isolate Q.

The inequality states that
`\(-(Q)/(7) \geq -1\)`, implying that Q divided by 7 is greater than or equal to -1.

To solve for Q, we'll first multiply both sides of the inequality by -7 to eliminate the fraction and isolate Q:

`\(-7 * \left(-(Q)/(7)\right) \geq -1 * (-7)\)`

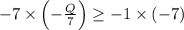
This simplifies to:

`\(Q \leq 7\)`

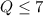
Therefore, the solution to the inequality
`\(-(Q)/(7) \geq -1\)` is
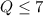`\(Q \leq 7\)`. This implies that any value of Q that is less than or equal to 7 will satisfy the inequality.

Graphically, this solution represents all values of Q that are less than or equal to 7 on a number line, including 7 itself. If Q takes any value less than or equal to 7, it will make the original inequality
`\(-(Q)/(7) \geq -1\)` true.

In essence, the inequality solution
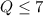`\(Q \leq 7\)` denotes a range of values for Q that satisfy the given inequality, ensuring that the expression on the left side of the inequality is greater than or equal to the value on the right side.

Question:

What is the solution to the inequality
`\(-(Q)/(7) \geq -1\)`?