Question

F(16) as a linear function

Answer 1

The function
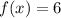`\(f(x) = 6\)` is a constant, representing a horizontal line at
`\(y = 6\)`. It's a linear function but lacks a slope or rate of change, maintaining a constant value of
`\(6\)` for all
`\(x\)`.

The function
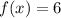`\(f(x) = 6\)` represents a constant function where the output (or
`\(y\)-value)` is always
`\(6\)` regardless of the input (or
`\(x\)-value`).

In this case, the function doesn't have a variable term
`(\(x\))` or any slope because it's a horizontal line parallel to the x-axis at a height of
`\(y = 6\)`.

Given function :
`\(f(x) = 6\)`

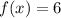
Explanation: The function is a horizontal line at
`\(y = 6\)` on the Cartesian plane.

Slope: Not applicable as the function doesn't have a variable term
`(\(x\))` to determine a slope. It's a constant function, so there's no change in
`\(y\)` with respect to
`\(x\)`.

Rate of change: There's no rate of change since the function's output remains constantly
`\(6\)` for all
`\(x\)` values.

Therefore, the function
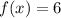`\(f(x) = 6\)` is indeed a linear function (a horizontal line), but it doesn't have a slope or a rate of change as it represents a constant value of
`\(6\)`.

complete the question

Is f(x) 6 a linear function?

Yes, f(x) 6 is a linear function.

No, f(x) = 6 is not a linear function.

If so, what are the slope and the rate of change? (If the function is not linear, enter NOT LINEAR.)