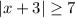The solution to the inequality
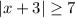 is
is
 or
or
 .
.
To solve the inequality
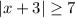 , we can break it into two cases based on the expression within the absolute value:
, we can break it into two cases based on the expression within the absolute value:
1. Case 1:
![\(x + 3 \geq 7\) \[x + 3 \geq 7\]](https://img.qammunity.org/2024/formulas/mathematics/college/yr8l4pshir3bua438l799n57kwmyos7lv5.png)
Subtract 3 from both sides:
![\[x \geq 4\]](https://img.qammunity.org/2024/formulas/mathematics/college/ups6fru81mf3n8pfgyf016zucnsurqnl4g.png)
2. Case 2:
![\(-(x + 3) \geq 7\) \[-(x + 3) \geq 7\]](https://img.qammunity.org/2024/formulas/mathematics/college/if9a2365wvo10uoyjrey1earq1ld8qy3k1.png)
Distribute the negative sign:
![\[-x - 3 \geq 7\]](https://img.qammunity.org/2024/formulas/mathematics/college/ob3rvjimfknfezl26s6s6c7i29ns305rki.png)
Add 3 to both sides:
![\[-x \geq 10\]](https://img.qammunity.org/2024/formulas/mathematics/college/ewjquawsqkochhe9iijj7h9w7ohebzuu00.png)
Multiply both sides by
 (reverse the inequality sign when multiplying by a negative number):
(reverse the inequality sign when multiplying by a negative number):
![\[x \leq -10\]](https://img.qammunity.org/2024/formulas/mathematics/college/3stzbcw6tfcqlpmo18a33a7sdh5biyim70.png)
So, the solution to the inequality
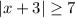 is
is
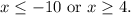
The complete question is:
Solving linear inequalities
Look at the following inequality,