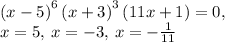Question

How to differentiate this?​

Answer 1

`\left(x-5\right)^6\left(x+3\right)^3\left(11x+1\right)`

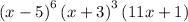
and

`x=5,\:x=-3,\:x=-(1)/(11)`

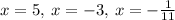
Explanation:

This problem is slightly more difficult.

We start off with the product rule. If y = v*u then in the case:

`u=\left(x+3\right)^4,\:v=\left(x-5\right)^7`

`=> (d)/(dx)\left(\left(x+3\right)^4\right)\left(x-5\right)^7+(d)/(dx)\left(\left(x-5\right)^7\right)\left(x+3\right)^4`

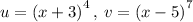
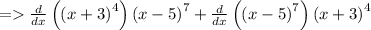
Now we apply the chain rule:

`(d)/(dx)\left(\left(x+3\right)^4\right) = 4\left(x+3\right)^3(d)/(dx)\left(x+3\right)\\= 4\left(x+3\right)^3\cdot \:1\\= 4\left(x+3\right)^3`

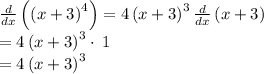
We can apply the chain rule again for this second bit:

`(d)/(dx)\left(\left(x-5\right)^7\right) = 7\left(x-5\right)^6(d)/(dx)\left(x-5\right)\\= 7\left(x-5\right)^6\cdot \:1\\= 7\left(x-5\right)^6`

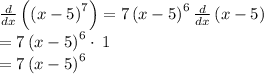
So now we are left with this long equation:

`4\left(x+3\right)^3\left(x-5\right)^7+7\left(x-5\right)^6\left(x+3\right)^4`

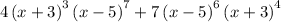
Which we can actually factor:

`4\left(x+3\right)^3\left(x-5\right)^7+7\left(x-5\right)^6\left(x+3\right)^4 = \left(x-5\right)^6\left(x+3\right)^3\left(4\left(x-5\right)+7\left(x+3\right)\right) \\= \left(x-5\right)^6\left(x+3\right)^3\left(11x+1\right)`

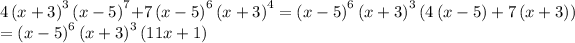
...And for the second bit, if we equate to 0, we can apply the Zero Product Property to get all the x values:

`\left(x-5\right)^6\left(x+3\right)^3\left(11x+1\right)=0,\\x=5,\:x=-3,\:x=-(1)/(11)`