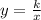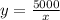Answer:
 and
and
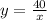
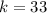 and
and
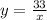
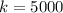 and
and
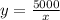
Explanation:
Given
y varies inversely with x.
This is represented as:
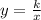
Where k is the constant of proportionality.
(a):
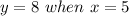
This gives:
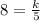

 -- the constant of proportionality.
-- the constant of proportionality.
To calculate the function, substitute 40 for k in
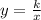
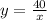
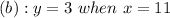
This gives:

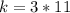
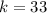 -- the constant of proportionality.
-- the constant of proportionality.
To calculate the function, substitute 33 for k in
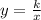
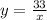
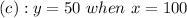
This gives:


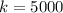 -- the constant of proportionality.
-- the constant of proportionality.
To calculate the function, substitute 5000 for k in