Question

-x^3 - 3x^2 = 6x + 4

Find all real and complex solutions of the polynomial equation.

Answer 1

The solutions to the equation are
`\(x = -2, 2, -1\)`


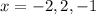
To find the solutions of the given polynomial equation
`\(-x^3 - 3x^2 = 6x + 4\)`, let's set the equation to zero and then try to factor it or use other methods:

`\[ -x^3 - 3x^2 - 6x - 4 = 0 \]`

Now, to find the solutions, you can try factoring or use numerical methods like the Rational Root Theorem, or you can use a computational tool. Factoring may not be straightforward, so let's consider a numerical approach.

By trying different values for x that could potentially be solutions, you can find that x = -2 is a solution. Divide the polynomial by x + 2 to find the remaining quadratic factor:

`\[ -(x + 2)(x^2 - x - 2) = 0 \]`

Now, set each factor to zero:

1.
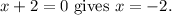
`\(x + 2 = 0\) gives \(x = -2\).`

2.
`\(x^2 - x - 2 = 0\)` can be factored or solved using the quadratic formula. Factoring gives
`\((x - 2)(x + 1) = 0\)`, so the solutions are x = 2 and x = -1.

Thus, the solutions to the equation are
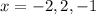`\(x = -2, 2, -1\)`.