compound interest, is an interest added to the "current stored amount" whatever that happens to be, bearing in mind that the current amount includes accrued interest from before, so if you had $10 and it compounds year at 10%, after a year you'd have $10 plus 10% of $10, or namely $11, the second year however, you'd get $11 plus 10% of $11, not $10 and so on, so is more money clearly, that's compound interest.
simple interest is a fixed amount of the original amount, so from $10 the next year at 10% you'd get $11, the next year after that you'd get $11 + 10% of $10 and so on.
looking at this table, we can see that the surplus amount from 2500 on the 1st year is 75 bucks, on the 2nd year is another 75 bucks, on the 3rd year another 75 bucks so is fixed value per year, namely is simple interest.
now if we know that 2500 is the 100%, what is 75 off of it in percentage?
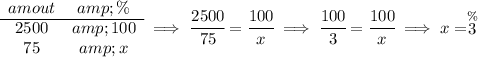
so let's plug those values in
![~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \$2500\\ r=rate\to 3\%\to (3)/(100)\dotfill &0.03\\ t=years\dotfill &t \end{cases} \\\\\\ A=2500[1+(0.03)(t)]\implies A=2500(1.003t)](https://img.qammunity.org/2023/formulas/mathematics/high-school/ld2o64p3wmkdk0bt6y29r5cj69d9p7dsqf.png)
how much will it be when t = 13?
![~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \$2500\\ r=rate\to 3\%\to (3)/(100)\dotfill &0.03\\ t=years\dotfill &13 \end{cases} \\\\\\ A=2500[1+(0.03)(13)]\implies A=3475](https://img.qammunity.org/2023/formulas/mathematics/high-school/b9490izpf34km6cd5a708g9y5heouuvfa5.png)