Final Answer:
the concentration of
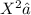 in a 0.100 M solution of the diprotic acid H2X is c.)
in a 0.100 M solution of the diprotic acid H2X is c.)
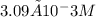
Step-by-step explanation:
In a 0.100 M solution of the diprotic acid H2X with dissociation constants
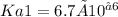 and
and
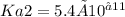 , we need to determine the concentration of
, we need to determine the concentration of
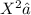 ions. The dissociation of H2X can be represented as follows:
ions. The dissociation of H2X can be represented as follows:
![\[H2X \rightleftharpoons H^+ + HX^- \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/tbubzj5245hqbj6zm8ghgscd2x0mislgtq.png)
![\[HX^- \rightleftharpoons H^+ + X^(2-)\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/xaowuvemakh5k3toho6a9ekjv8c3rwq806.png)
Let's denote the initial concentration of H2X as
![\([H2X]_0\)](https://img.qammunity.org/2024/formulas/chemistry/high-school/b9ehjjaccqtp20hqc0qaej3rw0hu85pwoo.png) and the change in concentration as x. The equilibrium concentrations can be expressed as
and the change in concentration as x. The equilibrium concentrations can be expressed as
![\([H2X]_0 - x\)](https://img.qammunity.org/2024/formulas/chemistry/high-school/em9z2618v9ioxluzgpo6o444i9n2w14b1b.png) ,
,
 , and
, and
 for H2X,
for H2X,
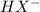 , and
, and
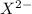 respectively.
respectively.
The equilibrium expression for the first dissociation is given by
![\(Ka1 = ([H^+][HX^-])/([H2X]_0 - x)\)](https://img.qammunity.org/2024/formulas/chemistry/high-school/ioskbd67ouqjecj6kr3h20gg7v9ab5hxpb.png) , and for the second dissociation,
, and for the second dissociation,
![\(Ka2 = ([H^+][X^(2-)])/([HX^-])\).](https://img.qammunity.org/2024/formulas/chemistry/high-school/ets9fej41835k5c5825xvckj3ljctq0tu9.png)
By solving these equations simultaneously, we find the concentration of
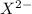 to be approximately
to be approximately
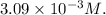
Therefore, the correct answer is option c)
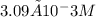 . This result is obtained through a systematic application of the principles of acid dissociation and equilibrium, ensuring accuracy in the determination of the concentration of
. This result is obtained through a systematic application of the principles of acid dissociation and equilibrium, ensuring accuracy in the determination of the concentration of
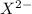 in the given diprotic acid solution.
in the given diprotic acid solution.