A statement that is true when using the converse of the Pythagorean theorem to determine if this is a right triangle is: B. We can set a equal to 20 or 15, and we can set b equal to 20 or 15. But we must set c equal to 25.
The converse of the Pythagorean theorem states that in a right angle triangle, the square of the third side of a triangle is equal to the sum of its two (2) shorter sides.
In Mathematics and Geometry, the converse of the Pythagorean's theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

Where:
- a is the opposite side of a right-angled triangle.
- b is the adjacent side of a right-angled triangle.
- c is the hypotenuse of a right-angled triangle.
Based on the converse of the Pythagorean theorem, we have:
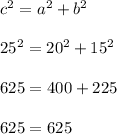
Complete Question:
A triangle has side lengths of 20, 15, and 25. Which of the following statements is true when using the converse of the Pythagorean theorem to determine if this is a right triangle?
We must set a = 15, b = 20, and c = 25 because this is increasing order for the numbers.
We can set a equal to 20 or 15, and we can set b equal to 20 or 15. But we must set c equal to 25.
We can set c = 20 or 25, and we can set a 20 or 25. But we must set b = 15.
We must set a = 20, b = 15, and c = 25 because this is the order in which the numbers appear