A height of 96 meters, the base of the cross-section is approximately 154 meters.
To find the dimensions of the cross-section at a height of 96 meters, you can use similar triangles formed by the original pyramid and the dilated cross-section.
Given:
Original height of the pyramid = 144 meters
Base length of the pyramid = 231 meters
Height of the cross-section = 96 meters
First, let's find the ratio of the height of the cross-section to the original height of the pyramid:
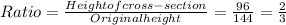
Now, since the cross-section is a dilation of the base at a certain height, the ratio of the corresponding sides of the pyramid and the cross-section will be the same.
The base length of the cross-section can be found using this ratio:
Base length of cross-section=
 ×Base length of pyramid
×Base length of pyramid
Base length of cross-section=
 ×231meters=154meters
×231meters=154meters
Therefore, at a height of 96 meters, the base of the cross-section is approximately 154 meters.