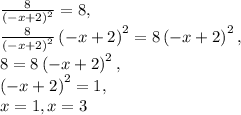Question

How do I differentiate this?​

Answer 1

`(8)/(\left(-x+2\right)^2)` &
`x = 1, x = 3`

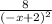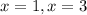
Explanation:

I'm sure you are familiar with the product rule,

If y = u*v => dy/dx = u * dv/dx + v * dy/dx <----- product rule

In this case:

`u=3x+2,\:v=\left(2-x\right)^(-1),\\=>(d)/(dx)\left(3x+2\right)\left(2-x\right)^(-1)+(d)/(dx)\left(\left(2-x\right)^(-1)\right)\left(3x+2\right)`

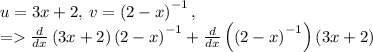
Now remember the sum rule:

`(d)/(dx)\left(3x+2\right) = (d)/(dx)\left(3x\right)+(d)/(dx)\left(2\right),\\(d)/(dx)\left(3x\right) = 3,\\(d)/(dx)\left(2\right) = 0\\(d)/(dx)\left(3x+2\right) = 3`

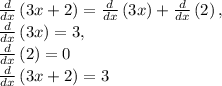
For this second bit we apply the chain rule:

`(d)/(dx)\left(\left(2-x\right)^(-1)\right) = -(1)/(\left(2-x\right)^2)(d)/(dx)\left(2-x\right),\\(d)/(dx)\left(2-x\right) = -1,\\\\=> -(1)/(\left(2-x\right)^2)\left(-1\right)\\=> (1)/(\left(2-x\right)^2)`

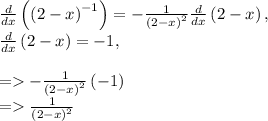
If we substitute these values back into the expression...
`(d)/(dx)\left(3x+2\right)\left(2-x\right)^(-1)+(d)/(dx)\left(\left(2-x\right)^(-1)\right)\left(3x+2\right)`

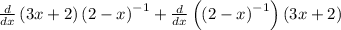
...we get the following:

`3\left(2-x\right)^(-1)+(1)/(\left(2-x\right)^2)\left(3x+2\right)`

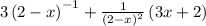
The rest is just pure simplification:

`3\left(2-x\right)^(-1)+(1)/(\left(2-x\right)^2)\left(3x+2\right)\\= (3)/(-x+2)+(3x+2)/(\left(-x+2\right)^2)\\= (3\left(-x+2\right))/(\left(-x+2\right)^2)+(3x+2)/(\left(-x+2\right)^2)\\\\= (3\left(-x+2\right)+3x+2)/(\left(-x+2\right)^2)\\\\= (8)/(\left(-x+2\right)^2)`

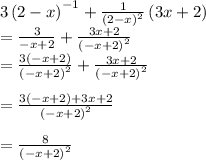
Now let's equate this to equal 8 for the second bit and solve for x:

`(8)/(\left(-x+2\right)^2)=8,\\(8)/(\left(-x+2\right)^2)\left(-x+2\right)^2=8\left(-x+2\right)^2,\\8=8\left(-x+2\right)^2,\\\left(-x+2\right)^2=1,\\x = 1, x = 3`